Generate Random Points in a Circle

Motivation

I found this problem on Leetcode while going through Geometry problems. So my first intuition was the most simple one, which everyone would get upon reading the problem for the first time. Unfortunately, that didn't work out, and I had no idea why. So I went on to extend the program to visualize my solution. Check out the source code here.

Try it out with your own ideas before checking out the correct approach!

Problem Statement

So the problem requires you to write a function that generates random points that are evenly distributed inside a circle of a given radius.

Suppose you are given a circle of radius R and the the center of the circle is (x_center, y_center). Your objective is to write a function randPoint which returns [random_x, random_y] when invoked and is then used to generate N points inside the circle which are distributed evenly.

You can try solving and visualizing this in a programming language of your choice but I would recommend Python given the availability of the Matplotlib library. If using Python you can use this template if you want to use my program to visualize your solution.

Just edit the randPoint function with your logic to generate the coordinates. The plot function is already written and the source code can be found here.

class Solution:
    def __init__(self, radius: float, x_center: float, y_center: float):
        self.radius = radius
        self.x_center = x_center
        self.y_center = y_center

    def randPoint(self) -> list[float]:
        x = "Expression to generate x coordinate"
        y = "Expression to generate y coordinate"
        return [x, y]

    def plot(self, description):
      # Calls randPoint func and plots your solution
      pass

You can use the following code to instantiate this class and generate the plot:

radius = 5
s = Solution(radius, 0, 0)
s.plot("• Plot description")

After you are done writing the logic you can run the script. Before running make sure you install the dependencies.

pip3 install numpy matplotlib
python3 circle.py

This is what a uniform distribution looks like:

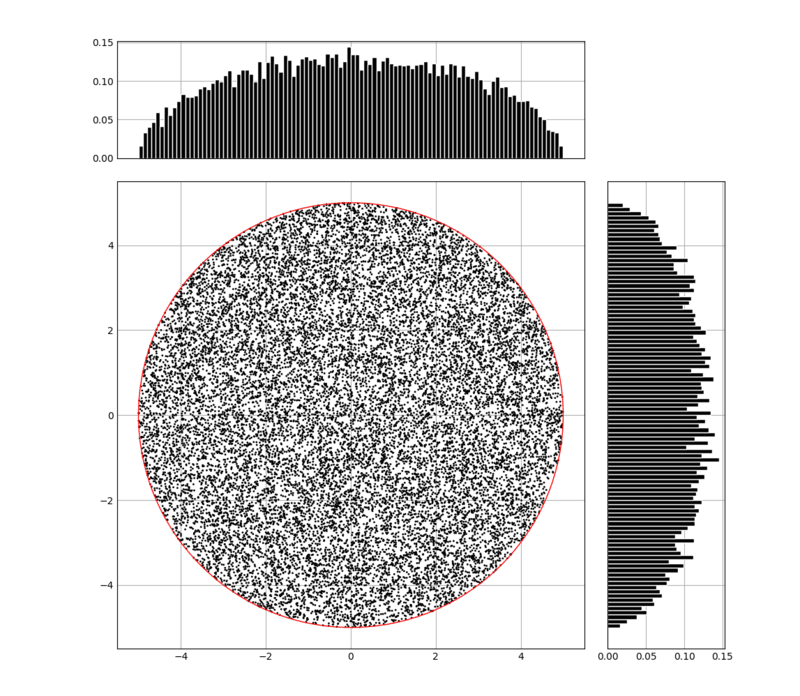
Give this a try before heading over to the solution.

Solution

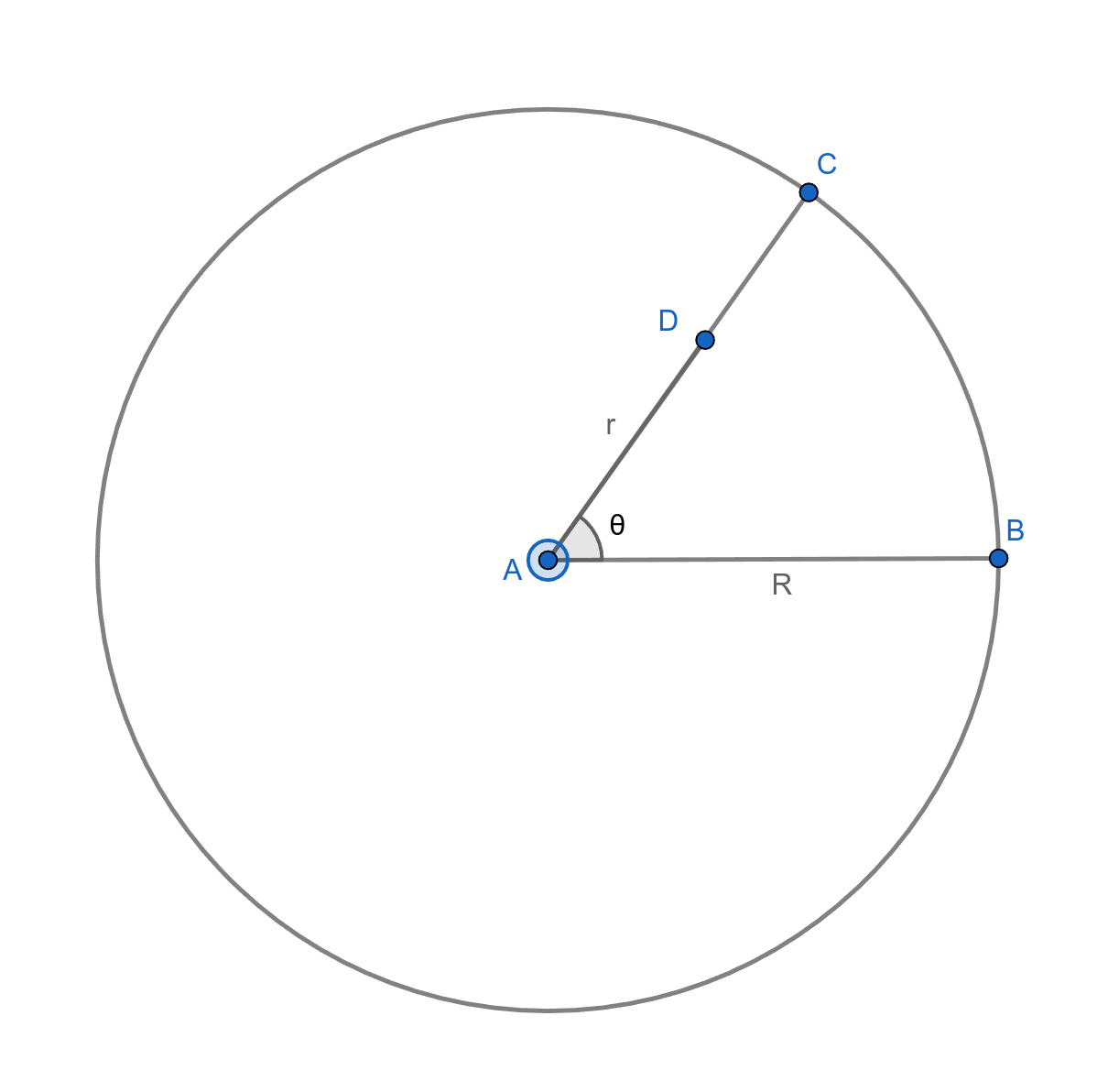
So after reading this problem, my naive first thought was to select a random angle θ between [0, 2π] and then choose a distance r between [0, R]. That would give a random point on the circle.

Here's an illustration of the approach:

Let's code up this approach:

def randPoint(self) -> list[float]:
    r = random.uniform(0, self.radius)
    theta = 2 * math.pi * random.uniform(0, 1)
    x = self.x_center + r * math.cos(theta)
    y = self.y_center + r * math.sin(theta)
    return [x, y]

The position of a chosen point relative to the center of the circle is (rcos(θ),rsin(θ)). Here (x,y) is returned relative to the origin.

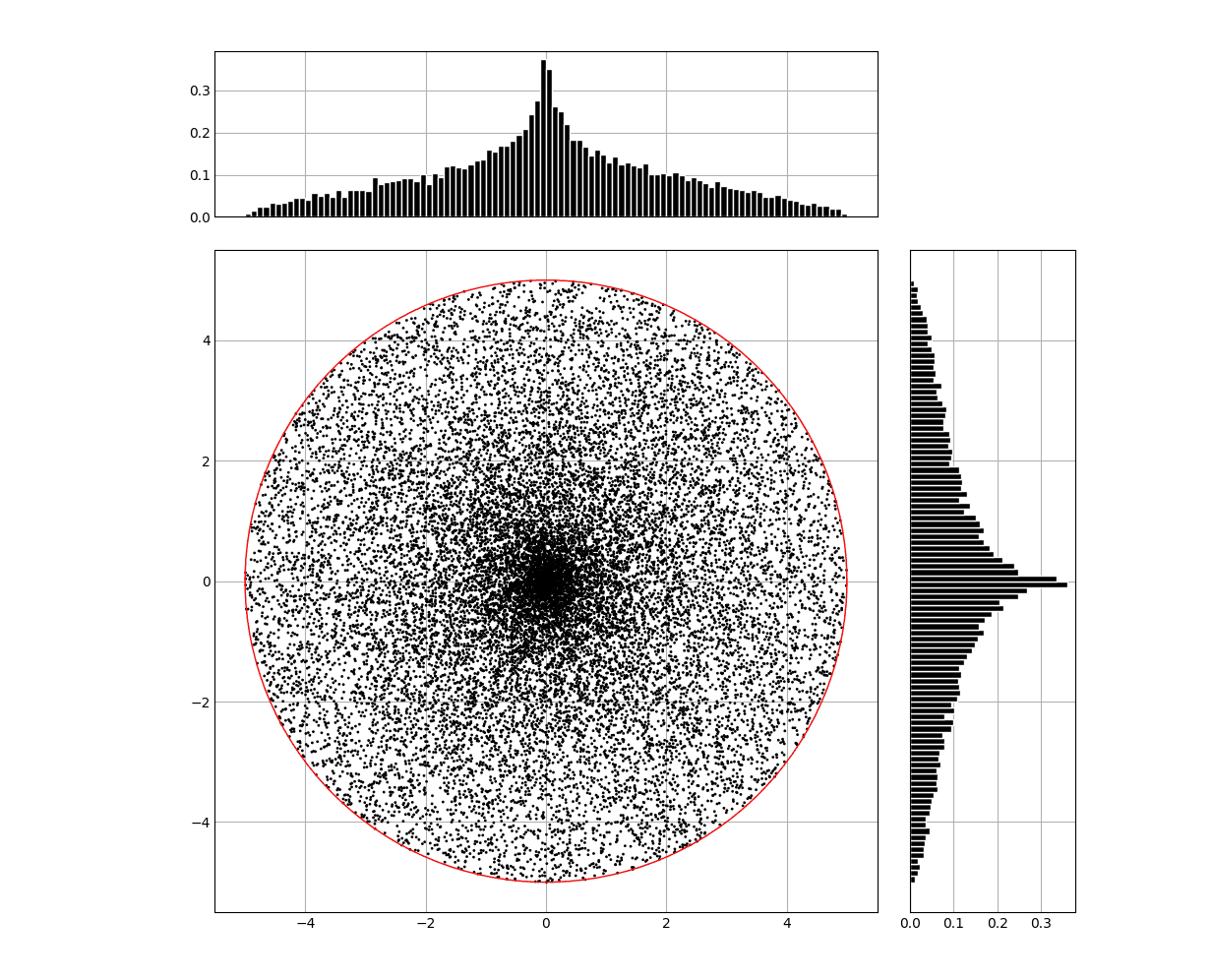
Now let's try to plot the points generated this way:

We can already make out that this distribution isn't uniform. But what went wrong?

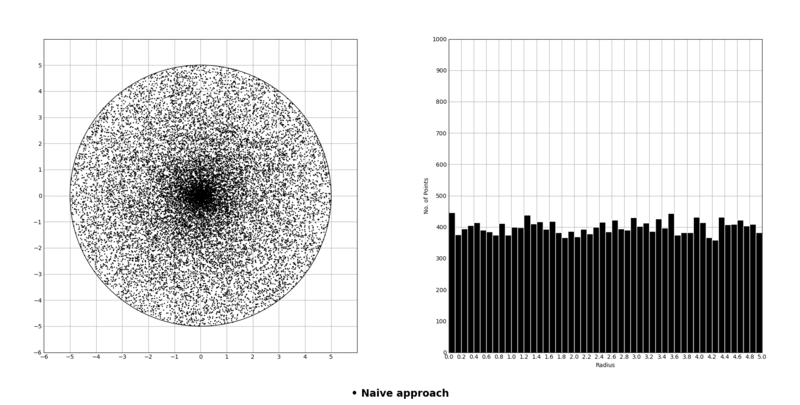
The second sub-figure shows the distribution of points with radius. We can see that this distribution is uniform which means that the density of points is same for all r from [0, R]. This is why we got more points near the center as illustrated in this figure:

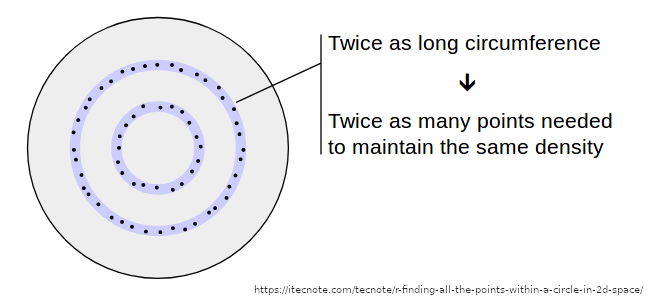
So this approach didn't work out, which made me think of a totally different approach.

Let's start with what we can generate randomly. So I looked up the Python documentation for the random module and came across a function of interest:

random.uniform(a, b): Return a random floating point number N such that a <= N <= b for a <= b and b <= N <= a for b < a.

So geometrically we can generate a random point on a line segment of length l using:

x = l * random.uniform(0, 1)

We can extend this to generate a point inside a square of length l just by adding a y dimension:

x = l * random.uniform(0, 1)
y = l * random.uniform(0, 1)

Now, how can we use this to solve the original problem?

Let's generate points inside a square that encloses the circle of radius R. The side of this square will be 2R. You can already sense where we are trying to go with this. So after we generate a random point inside the enclosing square, we just check if it lies inside the circle. If it does, well and good. Otherwise, we keep generating new points until we get a valid point.

Let's code this up:

def randPoint(self) -> list[float]:
    while True:
        rand_y = random.uniform(-self.radius, self.radius)
        rand_x = random.uniform(-self.radius, self.radius)
        if rand_x**2 + rand_y**2 <= self.radius**2:
            break
    x = self.x_center + rand_x
    y = self.y_center + rand_y
    return [x, y]

The code is self-explanatory, we keep generating points unless it lies inside the circle. We check if a point is inside a circle by checking if the distance of that point from the center is less than or equal to the radius.

Now you must be wondering why this works. The answer lies in the previous diagram itself, we can see that if we select any smaller area than the square, the points that are uniformly distributed inside the square will be uniformly distributed over the smaller area provided that point lies within the smaller area.

Let's see how the plot looks now:

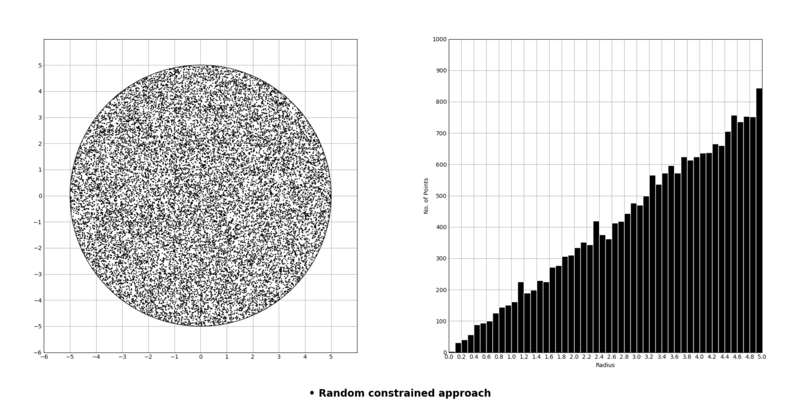
Perfect!

When I first came up with this solution I thought this was just a hack, but turns out it is an established statistical concept known as rejection sampling.

Rejection sampling is a Monte Carlo algorithm to sample data from a sophisticated (“difficult to sample from”) distribution with the help of a proxy distribution.

Now back to the generated plot, we can notice that the number of points grows linearly with radius. This confirms our hypothesis that the number of points should scale linearly with the circumference 2πr.

Turns out we could have used this knowledge to define a distribution function using a method called inverse transform sampling. This requires an intermediate knowledge of statistics and is thus kept out of the scope of this article. But you can read more about this approach here.

The code for this approach looks like this:

def randPoint(self) -> list[float]:
    theta = random.uniform(0, 2 * math.pi)
    R = math.sqrt(random.uniform(0, self.radius**2))
    return [
        self.x_center + R * math.cos(theta),
        self.y_center + R * math.sin(theta),
    ]

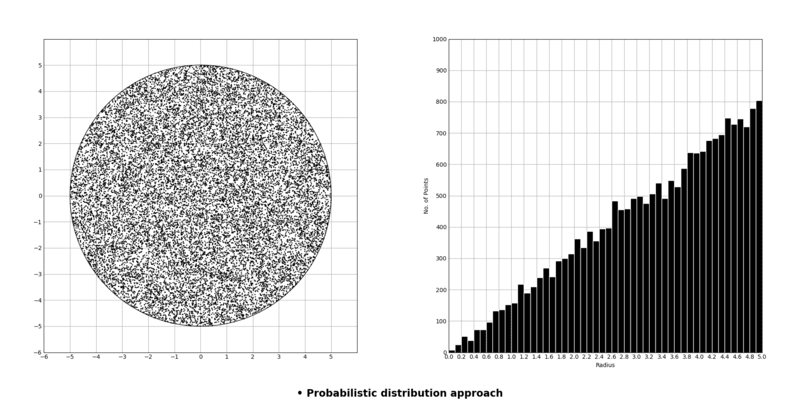
We get the same uniform plot:

Conclusion

We went over two different approaches on how to solve this problem. While the rejection sampling method was more intuitive, it is not as performant as the distribution function approach. Let me know which one you liked more. If you’ve got a comment to share, reach out to me on any social media platform or email.

If you found this article valuable, share it with your friends. Stay curious!