Solving JEE Advanced Problems in Python: Exploring Binomial Expansion


6 min, 1193 words

Categories: Maths Python

Tags: python maths


jee-binomial-meme

How it started?

Problem

Today, we will examine a problem that appeared in JEE Advanced 2016, specifically in Paper I as problem number 51 in the Part III: Mathematics section. You can find the official question paper linked here.

Now, let's dive into the problem:

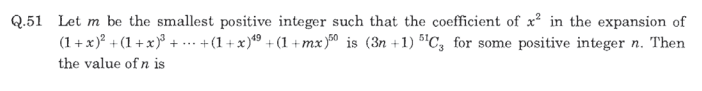
jee problem

Converting the problem to LaTeX:

Let \( m \) be the smallest positive integer such that the coefficient of \( x^2 \) in the expansion of $$ (1+x)^{2}+(1+x)^{3}+\cdots+(1+x)^{49}+(1+mx)^{50} $$ is \( (3n+1)^{51}C_{3} \) for some positive integer n. Then the value of \( n \) is

Binomial Theorem

The binomial theorem is a mathematical formula that expresses the expansion of a power of the sum of two numbers. It states that the expansion of \( (a+b)^n \) can be expressed as a sum of terms, each of which is the product of a binomial coefficient and powers of \( a \) and \( b \).

The binomial coefficient, denoted by \( {n \choose k} \), is the number of ways to choose \( k \) objects from a set of \( n \) objects. The formula for the binomial theorem is:

$$(a+b)^n = \sum_{k=0}^{n} {n \choose k} a^{n-k} b^k$$

where \( {n \choose k} = \frac{n!}{k!(n-k)!} \).

Special case

For the expansion of \( (1+mx)^n \), \( a=1 \) and \( b=mx \), the binomial theorem becomes:

$$(1+mx)^n = \sum_{k=0}^{n} {n \choose k} 1^{n-k} (mx)^k$$

Simplifying, we get:

$$(1+mx)^n = \sum_{k=0}^{n} {n \choose k} m^k x^k$$

Therefore, the coefficient of \( x^k \) in the expansion of \( (1+mx)^n \) is \( {n \choose k} (m^k) \).

Python Implementation

Let's try to implement a recursive solution which doesn't assume the knowledge of binomial theorem.

We have to compute the coefficient of \( x^p \) in \( (1 + mx)^n \). We have,

$$(1+mx)^n = (1+mx)^{n-1} \cdot (1+mx)$$

Recursive Case:

  • The coefficient for \( x^p \) in \( (1 + mx)^n \) can be computed by summing:
    • The coefficient of \( x^p \) in \( (1 + mx)^{n-1} \)
    • The coefficient of \( x^{p-1} \) in \( (1 + mx)^{n-1} \) multiplied by \( m \)

Base Cases:

  • If \( p == 0 \), the coefficient is \( 1 \) (the constant term).
  • If \( p > n \), the coefficient is \( 0 \) (there aren't enough \( x \) terms).
  • If \( p == n \), the coefficient is \( m^n \) (the case where all terms are \( x \)).

Here's how we can implement it in Python:

# Coeff of x^p in (1+mx)^n

def coeff(m, n, p):
    if p == 0:
        return 1
    elif p > n:
        return 0
    elif p == n:
        return pow(m, n)
    return coeff(m, n - 1, p) + m * coeff(m, n - 1, p - 1)


print(coeff(1, 2, 0))
print(coeff(1, 2, 1))
print(coeff(1, 2, 2))

As \( (1+x)^2 = 1 + 2 \cdot x + x^2 \) the output is:

1
2
1

Optimizations

Experienced competitive programmers reading this code would be smelling exponential time complexity due to overlapping subproblems. Let's put a dirty one-liner hotfix to resolve this:

# Optimized coeff of x^p in (1+mx)^n
import functools

@functools.cache
def coeff(m, n, p):
    if p == 0:
        return 1
    if p > n:
        return 0
    elif p == n:
        return pow(m, n)
    return coeff(m, n - 1, p) + m * coeff(m, n - 1, p - 1)

Better? We can improve further by implementing this using an iterative approach but this would suffice for now.

functools.cache meme

Using math.comb() to find the coefficient

We can also take advantage of the binomial theorem to get the coefficient. Here's how:

As the coefficient of \( x^k \) in the expansion of \( (1+mx)^n \) is given by \( {n \choose k} (m^k) \).

# Coeff of x^p in (1+mx)^n
from math import comb

def coeff_binomial(m, n, p):
    if p > n:
        return 0
    return comb(n, p) * pow(m, p)

Solution

Enough with the fun! Now that we have an efficient coefficient function, let's get the problem out of the way. We had the coefficient of \( x^2 \) in the expansion of:

$$ (1+x)^{2}+(1+x)^{3}+\cdots+(1+x)^{49}+(1+mx)^{50} = (3n+1)^{51}C_{3} $$

where \( m, n \in \mathbb{Z}^+\) and minimize m.

Let's calculate the coefficient of \( x^2 \) in the expansion leaving the last term as \( m \) is currently unknown:

from math import comb

coeff_x2 = sum([coeff(1, i, 2) for i in range(2, 50)])
c_51_3 = comb(51, 3)

We also calculate \( {51}C_{3} \) which will come in handy soon. Now let's brute search for m starting from 1. If you have made it this far then the code should be self-explanatory.

for m in range(1, 100):
    lhs = coeff_x2 + coeff(m, 50, 2)

    if lhs % c_51_3 == 0:
        quotient = lhs // c_51_3
        if quotient % 3 == 1 and quotient // 3 != 0:
            n = (quotient - 1) // 3
            print(f"Answer is: {n}")
            break

Output

animesh@pop-os:~$ python -u "/home/animesh/jee.py"
Answer is: 5

The answer indeed is 5 and luckily the problem isn't that difficult even when solving using pen/paper. Give it a try!

Conclusion

Although using a programming language seems fun for solving these types of problems, pen-and-paper methods are often more effective for standard problems. Working on JEE problems with Python can enhance your understanding of both programming and mathematical concepts 😉

References

  1. JEE (Advanced) Archive
  2. Binomial theorem - Wikipedia
  3. functools — Python 3.13.0 documentation

Stay Tuned

Hope you enjoyed reading this. Stay tuned for more cool stuff coming your way!